|
Gromacs
2018.8
|
|
Gromacs
2018.8
|
#include <gromacs/tables/quadraticsplinetable.h>
Quadratic spline interpolation table.
This class interpolates a function specified either as an analytical expression or from user-provided table data.
At initialization, you provide the reference function of vectors as a list of tuples that contain a brief name, the function, and derivative for each function to tabulate. To create a table with two functions this initializer list can for instance look like
{ {"LJ6", lj6Func, lj6Der}, {"LJ12", lj12Func, lj12Der} }
The names are only used so exceptions during initialization can be traced to a specific table.
When interpolating, there are methods to interpolate either 1, 2, or 3 functions in one go. By default these interpolation routines will operate on tables with the same number of functions as specified in the interpolation method (debug builds check that this is consistent with the table). However, it is also possible to use optional template parameters that specify the total number of functions in a table, and what function index to interpolate. For instance, to interpolate the derivative of the second function (i.e., index 1) in a multi-function-table with three functions in total, you can write
table.evaluateDerivative<3,1>(x,&der);
Here too, debug builds will check that the template parameters are consistent with the table.
The table data is internally adjusted to guarantee that the interpolated derivative is the true derivative of the interpolated potential, which is important to avoid systematic errors for the common case when the derivative is concave/convex in the entire interval. We do this by expressing the difference in the function value at a small offset h relative to a reference value in position 0 with a forward Taylor series expanded around 0, and then doing the opposite of expressing difference in the function at position 0 relative to a reference value in position h when using a backward Taylor expansion:
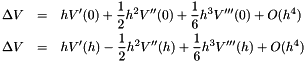
Summing the equations leads to
![\[ 2 \Delta V = h(V'(0) + V'(h)) + \frac{1}{2} h^2 (V''(0)-V''(h)) + \frac{1}{6}h^3(V'''(0)+V'''(h)) + O(h^4) \]](form_52.png)
To make the second term symmetric too, we can replace it with the average of the Taylor expansion at 0 and h (i.e., using the third derivative). This gives
![\[ 2 \Delta V = h(V'(0) + V'(h)) - \frac{1}{12} h^3 (V'''(0)+V'''(h)) + O(h^4) \]](form_53.png)
Thus, if we replace the derivative in the internal quadratic table data with
![\[ V' - \frac{1}{12}h^2 V''' \]](form_54.png)
we will cancel the h^3 term in the error. This will make the integral of the forces match the potential much better (The h^4 term actually disappears, so when summing over 1/h points the remaining error will be O(h^4).
While it is possible to create tables only from function values (i.e., no derivatives), it is recommended to provide derivatives for higher accuracy and to avoid issues with numerical differentiation. Note that the table input should be smooth, i.e. it should not contain noise e.g. from an (iterative) Boltzmann inversion procedure - you have been warned.
Public Member Functions | |
| QuadraticSplineTable (std::initializer_list< AnalyticalSplineTableInput > analyticalInputList, const std::pair< real, real > &range, real tolerance=defaultTolerance) | |
| Initialize table data from function. More... | |
| QuadraticSplineTable (std::initializer_list< NumericalSplineTableInput > numericalInputList, const std::pair< real, real > &range, real tolerance=defaultTolerance) | |
| Initialize table data from tabulated values and derivatives. More... | |
| template<int numFuncInTable = 1, int funcIndex = 0, typename T > | |
| void | evaluateFunctionAndDerivative (T r, T *functionValue, T *derivativeValue) const |
| Evaluate both function and derivative, single table function. More... | |
| template<int numFuncInTable = 1, int funcIndex = 0, typename T > | |
| void | evaluateFunction (T r, T *functionValue) const |
| Evaluate function value only, single table function. More... | |
| template<int numFuncInTable = 1, int funcIndex = 0, typename T > | |
| void | evaluateDerivative (T r, T *derivativeValue) const |
| Evaluate function derivative only, single table function. More... | |
| template<int numFuncInTable = 2, int funcIndex0 = 0, int funcIndex1 = 1, typename T > | |
| void | evaluateFunctionAndDerivative (T r, T *functionValue1, T *derivativeValue1, T *functionValue2, T *derivativeValue2) const |
| Evaluate both function and derivative, two table functions. More... | |
| template<int numFuncInTable = 2, int funcIndex0 = 0, int funcIndex1 = 1, typename T > | |
| void | evaluateFunction (T r, T *functionValue1, T *functionValue2) const |
| Evaluate function value only, two table functions. More... | |
| template<int numFuncInTable = 2, int funcIndex0 = 0, int funcIndex1 = 1, typename T > | |
| void | evaluateDerivative (T r, T *derivativeValue1, T *derivativeValue2) const |
| Evaluate function derivative only, two table functions. More... | |
| template<int numFuncInTable = 3, int funcIndex0 = 0, int funcIndex1 = 1, int funcIndex2 = 2, typename T > | |
| void | evaluateFunctionAndDerivative (T r, T *functionValue1, T *derivativeValue1, T *functionValue2, T *derivativeValue2, T *functionValue3, T *derivativeValue3) const |
| Evaluate both function and derivative, three table functions. More... | |
| template<int numFuncInTable = 3, int funcIndex0 = 0, int funcIndex1 = 1, int funcIndex2 = 2, typename T > | |
| void | evaluateFunction (T r, T *functionValue1, T *functionValue2, T *functionValue3) const |
| Evaluate function value only, three table functions. More... | |
| template<int numFuncInTable = 3, int funcIndex0 = 0, int funcIndex1 = 1, int funcIndex2 = 2, typename T > | |
| void | evaluateDerivative (T r, T *derivativeValue1, T *derivativeValue2, T *derivativeValue3) const |
| Evaluate function derivative only, three table functions. More... | |
| real | tableSpacing () const |
| Return the table spacing (distance between points) More... | |
Static Public Attributes | |
| static const real | defaultTolerance = 10.0 * 1.19209290e-07F |
| Default tolerance for tables is 10*GMX_FLOAT_EPS. More... | |
| gmx::QuadraticSplineTable::QuadraticSplineTable | ( | std::initializer_list< AnalyticalSplineTableInput > | analyticalInputList, |
| const std::pair< real, real > & | range, | ||
| real | tolerance = defaultTolerance |
||
| ) |
Initialize table data from function.
| analyticalInputList | Initializer list with one or more functions to tabulate, specified as pairs containing analytical functions and their derivatives. The function will also be called for values smaller than the lower limit of the range, but we avoid calling it for 0.0 if that value is not included in the range. |
| range | Range over which the function will be tabulated. Constructor will throw gmx::APIError for negative values. Due to the way the numerical derivative evaluation depends on machine precision internally, this range must be at least 0.001, or the constructor throws gmx::APIError. |
| tolerance | Requested accuracy of the table. This will be used to calculate the required internal spacing. If this cannot be achieved (for instance because the table would require too much memory) the constructor will throw gmx::ToleranceError. |
| gmx::ToleranceError | if the requested tolerance cannot be achieved, and gmx::APIError for other incorrect input. |
| gmx::QuadraticSplineTable::QuadraticSplineTable | ( | std::initializer_list< NumericalSplineTableInput > | numericalInputList, |
| const std::pair< real, real > & | range, | ||
| real | tolerance = defaultTolerance |
||
| ) |
Initialize table data from tabulated values and derivatives.
| numericalInputList | Initializer list with one or more functions to tabulate, specified as pairs containing containing vectors for the function values and their derivatives. Data points are separated by the spacing parameter, starting from 0. Values below the lower limit of the range will be used to attempt defining the table, but we avoid using index 0 unless 0.0 is included in the range. Some extra points beyond range.second are required to re-interpolate values, so add some margin. The constructor will throw gmx::APIError if the input vectors are too short to cover the requested range (and they must always be at least five points). |
| range | Range over which the function will be tabulated. Constructor will throw gmx::APIError for negative values, or if the value/derivative vector does not cover the range. |
| tolerance | Requested accuracy of the table in the range. This will be used to calculate the required internal spacing and possibly re-interpolate. The constructor will throw gmx::ToleranceError if the input spacing is too coarse to achieve this accuracy. |
|
inline |
Evaluate function derivative only, single table function.
This is a templated method where the template can be either real or SimdReal.
| numFuncInTable | Number of separate functions in table, default is 1 |
| funcIndex | Index of function to evaluate in table, default is 0 |
| T | Type (SimdReal or real) of lookup and result |
| r | Points for which to evaluate function derivative | |
| [out] | derivativeValue | Function derivative |
For debug builds we assert that the input values fall in the range specified when constructing the table.
|
inline |
Evaluate function derivative only, two table functions.
This is a templated method where the template can be either real or SimdReal.
| numFuncInTable | Number of separate functions in table, default is 2 |
| funcIndex0 | Index of 1st function to evaluate in table, default is 0 |
| funcIndex1 | Index of 2nd function to evaluate in table, default is 1 |
| T | Type (SimdReal or real) of lookup and result |
| r | Points for which to evaluate function derivative | |
| [out] | derivativeValue1 | Interpolated derivative for first function |
| [out] | derivativeValue2 | Interpolated derivative for second function |
For debug builds we assert that the input values fall in the range specified when constructing the table.
|
inline |
Evaluate function derivative only, three table functions.
This is a templated method where the template can be either real or SimdReal.
| numFuncInTable | Number of separate functions in table, default is 3 |
| funcIndex0 | Index of 1st function to evaluate in table, default is 0 |
| funcIndex1 | Index of 2nd function to evaluate in table, default is 1 |
| funcIndex2 | Index of 3rd function to evaluate in table, default is 2 |
| T | Type (SimdReal or real) of lookup and result |
| r | Points for which to evaluate function derivative | |
| [out] | derivativeValue1 | Interpolated derivative for first function |
| [out] | derivativeValue2 | Interpolated derivative for second function |
| [out] | derivativeValue3 | Interpolated derivative for third function |
For debug builds we assert that the input values fall in the range specified when constructing the table.
|
inline |
Evaluate function value only, single table function.
This is a templated method where the template can be either real or SimdReal.
| numFuncInTable | Number of separate functions in table, default is 1 |
| funcIndex | Index of function to evaluate in table, default is 0 |
| T | Type (SimdReal or real) of lookup and result |
| r | Points for which to evaluate function value | |
| [out] | functionValue | Function value |
For debug builds we assert that the input values fall in the range specified when constructing the table.
|
inline |
Evaluate function value only, two table functions.
This is a templated method where the template can be either real or SimdReal.
| numFuncInTable | Number of separate functions in table, default is 2 |
| funcIndex0 | Index of 1st function to evaluate in table, default is 0 |
| funcIndex1 | Index of 2nd function to evaluate in table, default is 1 |
| T | Type (SimdReal or real) of lookup and result |
| r | Points for which to evaluate function value | |
| [out] | functionValue1 | Interpolated value for first function |
| [out] | functionValue2 | Interpolated value for second function |
For debug builds we assert that the input values fall in the range specified when constructing the table.
|
inline |
Evaluate function value only, three table functions.
This is a templated method where the template can be either real or SimdReal.
| numFuncInTable | Number of separate functions in table, default is 3 |
| funcIndex0 | Index of 1st function to evaluate in table, default is 0 |
| funcIndex1 | Index of 2nd function to evaluate in table, default is 1 |
| funcIndex2 | Index of 3rd function to evaluate in table, default is 2 |
| T | Type (SimdReal or real) of lookup and result |
| r | Points for which to evaluate function value | |
| [out] | functionValue1 | Interpolated value for first function |
| [out] | functionValue2 | Interpolated value for second function |
| [out] | functionValue3 | Interpolated value for third function |
For debug builds we assert that the input values fall in the range specified when constructing the table.
|
inline |
Evaluate both function and derivative, single table function.
This is a templated method where the template can be either real or SimdReal.
| numFuncInTable | Number of separate functions in table, default is 1 |
| funcIndex | Index of function to evaluate in table, default is 0 |
| T | Type (SimdReal or real) of lookup and result |
| r | Points for which to evaluate function and derivative | |
| [out] | functionValue | Function value |
| [out] | derivativeValue | Function derivative |
For debug builds we assert that the input values fall in the range specified when constructing the table.
|
inline |
Evaluate both function and derivative, two table functions.
This is a templated method where the template can be either real or SimdReal.
| numFuncInTable | Number of separate functions in table, default is 2 |
| funcIndex0 | Index of 1st function to evaluate in table, default is 0 |
| funcIndex1 | Index of 2nd function to evaluate in table, default is 1 |
| T | Type (SimdReal or real) of lookup and result |
| r | Points for which to evaluate function and derivative | |
| [out] | functionValue1 | Interpolated value for first function |
| [out] | derivativeValue1 | Interpolated derivative for first function |
| [out] | functionValue2 | Interpolated value for second function |
| [out] | derivativeValue2 | Interpolated derivative for second function |
For debug builds we assert that the input values fall in the range specified when constructing the table.
|
inline |
Evaluate both function and derivative, three table functions.
This is a templated method where the template can be either real or SimdReal.
| numFuncInTable | Number of separate functions in table, default is 3 |
| funcIndex0 | Index of 1st function to evaluate in table, default is 0 |
| funcIndex1 | Index of 2nd function to evaluate in table, default is 1 |
| funcIndex2 | Index of 3rd function to evaluate in table, default is 2 |
| T | Type (SimdReal or real) of lookup and result |
| r | Points for which to evaluate function and derivative | |
| [out] | functionValue1 | Interpolated value for first function |
| [out] | derivativeValue1 | Interpolated derivative for first function |
| [out] | functionValue2 | Interpolated value for second function |
| [out] | derivativeValue2 | Interpolated derivative for second function |
| [out] | functionValue3 | Interpolated value for third function |
| [out] | derivativeValue3 | Interpolated derivative for third function |
For debug builds we assert that the input values fall in the range specified when constructing the table.
|
inline |
Return the table spacing (distance between points)
You should never have to use this for normal code, but due to the way tables are constructed internally we need this in the unit tests to check relative tolerances over each interval.
|
static |
Default tolerance for tables is 10*GMX_FLOAT_EPS.
 1.8.5
1.8.5