Removing fastest degrees of freedom¶
The maximum time step in MD simulations is limited by the smallest oscillation period that can be found in the simulated system. Bond-stretching vibrations are in their quantum-mechanical ground state and are therefore better represented by a constraint instead of a harmonic potential.
For the remaining degrees of freedom, the shortest oscillation period (as measured from a simulation) is 13 fs for bond-angle vibrations involving hydrogen atoms. Taking as a guideline that with a Verlet (leap-frog) integration scheme a minimum of 5 numerical integration steps should be performed per period of a harmonic oscillation in order to integrate it with reasonable accuracy, the maximum time step will be about 3 fs. Disregarding these very fast oscillations of period 13 fs, the next shortest periods are around 20 fs, which will allow a maximum time step of about 4 fs.
Removing the bond-angle degrees of freedom from hydrogen atoms can best be done by defining them as virtual interaction sites instead of normal atoms. Whereas a normal atom is connected to the molecule with bonds, angles and dihedrals, a virtual site’s position is calculated from the position of three nearby heavy atoms in a predefined manner (see also sec. Virtual interaction sites). For the hydrogens in water and in hydroxyl, sulfhydryl, or amine groups, no degrees of freedom can be removed, because rotational freedom should be preserved. The only other option available to slow down these motions is to increase the mass of the hydrogen atoms at the expense of the mass of the connected heavy atom. This will increase the moment of inertia of the water molecules and the hydroxyl, sulfhydryl, or amine groups, without affecting the equilibrium properties of the system and without affecting the dynamical properties too much. These constructions will shortly be described in sec. Hydrogen bond-angle vibrations and have previously been described in full detail 148.
Using both virtual sites and modified masses, the next bottleneck is likely to be formed by the improper dihedrals (which are used to preserve planarity or chirality of molecular groups) and the peptide dihedrals. The peptide dihedral cannot be changed without affecting the physical behavior of the protein. The improper dihedrals that preserve planarity mostly deal with aromatic residues. Bonds, angles, and dihedrals in these residues can also be replaced with somewhat elaborate virtual site constructions.
All modifications described in this section can be performed using the GROMACS topology building tool pdb2gmx. Separate options exist to increase hydrogen masses, virtualize all hydrogen atoms, or also virtualize the aromatic rings in standard residues. Note that when all hydrogen atoms are virtualized, those inside the aromatic residues will be virtualized as well, i.e. hydrogens in the aromatic residues are treated differently depending on the treatment of the aromatic residues. Note further that the virtualization of aromatic rings is deprecated.
Parameters for the virtual site constructions for the hydrogen atoms are inferred from the force-field parameters (vis. bond lengths and angles) directly by grompp while processing the topology file. The constructions for the aromatic residues are based on the bond lengths and angles for the geometry as described in the force fields, but these parameters are hard-coded into pdb2gmx due to the complex nature of the construction needed for a whole aromatic group.
Hydrogen bond-angle vibrations¶
Construction of virtual sites¶

Fig. 50 The different types of virtual site constructions used for hydrogen atoms. The atoms used in the construction of the virtual site(s) are depicted as black circles, virtual sites as gray ones. Hydrogens are smaller than heavy atoms. A: fixed bond angle, note that here the hydrogen is not a virtual site; B: in the plane of three atoms, with fixed distance; C: in the plane of three atoms, with fixed angle and distance; D: construction for amine groups (-NH\(_2\) or -NH\(_3^+\)), see text for details.¶
The goal of defining hydrogen atoms as virtual sites is to remove all high-frequency degrees of freedom from them. In some cases, not all degrees of freedom of a hydrogen atom should be removed, e.g. in the case of hydroxyl or amine groups the rotational freedom of the hydrogen atom(s) should be preserved. Care should be taken that no unwanted correlations are introduced by the construction of virtual sites, e.g. bond-angle vibration between the constructing atoms could translate into hydrogen bond-length vibration. Additionally, since virtual sites are by definition massless, in order to preserve total system mass, the mass of each hydrogen atom that is treated as virtual site should be added to the bonded heavy atom.
Taking into account these considerations, the hydrogen atoms in a protein naturally fall into several categories, each requiring a different approach (see also Fig. 50).
hydroxyl (-OH) or sulfhydryl (-SH) hydrogen: The only internal degree of freedom in a hydroxyl group that can be constrained is the bending of the C-O-H angle. This angle is fixed by defining an additional bond of appropriate length, see Fig. 50 A. Doing so removes the high-frequency angle bending, but leaves the dihedral rotational freedom. The same goes for a sulfhydryl group. Note that in these cases the hydrogen is not treated as a virtual site.
single amine or amide (-NH-) and aromatic hydrogens (-CH-): The position of these hydrogens cannot be constructed from a linear combination of bond vectors, because of the flexibility of the angle between the heavy atoms. Instead, the hydrogen atom is positioned at a fixed distance from the bonded heavy atom on a line going through the bonded heavy atom and a point on the line through both second bonded atoms, see Fig. 50 B.
planar amine (-NH\(_2\)) hydrogens: The method used for the single amide hydrogen is not well suited for planar amine groups, because no suitable two heavy atoms can be found to define the direction of the hydrogen atoms. Instead, the hydrogen is constructed at a fixed distance from the nitrogen atom, with a fixed angle to the carbon atom, in the plane defined by one of the other heavy atoms, see Fig. 50 C.
amine group (umbrella -NH\(_2\) or -NH\(_3^+\))* hydrogens:* Amine hydrogens with rotational freedom cannot be constructed as virtual sites from the heavy atoms they are connected to, since this would result in loss of the rotational freedom of the amine group. To preserve the rotational freedom while removing the hydrogen bond-angle degrees of freedom, two “dummy masses” are constructed with the same total mass, moment of inertia (for rotation around the C-N bond) and center of mass as the amine group. These dummy masses have no interaction with any other atom, except for the fact that they are connected to the carbon and to each other, resulting in a rigid triangle. From these three particles, the positions of the nitrogen and hydrogen atoms are constructed as linear combinations of the two carbon-mass vectors and their outer product, resulting in an amine group with rotational freedom intact, but without other internal degrees of freedom. See Fig. 50 D.
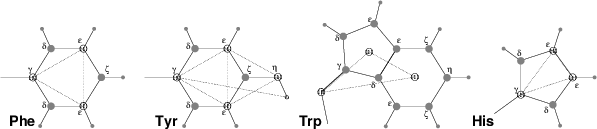
Fig. 51 The different types of virtual site constructions used for aromatic residues. The atoms used in the construction of the virtual site(s) are depicted as black circles, virtual sites as gray ones. Hydrogens are smaller than heavy atoms. A: phenylalanine; B: tyrosine (note that the hydroxyl hydrogen is not a virtual site); C: tryptophan; D: histidine.¶
Out-of-plane vibrations in aromatic groups¶
The planar arrangements in the side chains of the aromatic residues lends itself perfectly to a virtual-site construction, giving a perfectly planar group without the inherently unstable constraints that are necessary to keep normal atoms in a plane. The basic approach is to define three atoms or dummy masses with constraints between them to fix the geometry and create the rest of the atoms as simple virtual sites type (see sec. Virtual interaction sites) from these three. Each of the aromatic residues require a different approach:
Phenylalanine: C\(_\gamma\), C\(_{{\epsilon}1}\), and C\(_{{\epsilon}2}\) are kept as normal atoms, but with each a mass of one third the total mass of the phenyl group. See Fig. 50 A.
Tyrosine: The ring is treated identically to the phenylalanine ring. Additionally, constraints are defined between C\(_{{\epsilon}1}\), C\(_{{\epsilon}2}\), and O\(_{\eta}\). The original improper dihedral angles will keep both triangles (one for the ring and one with O\(_{\eta}\)) in a plane, but due to the larger moments of inertia this construction will be much more stable. The bond-angle in the hydroxyl group will be constrained by a constraint between C\(_\gamma\) and H\(_{\eta}\). Note that the hydrogen is not treated as a virtual site. See Fig. 50 B.
Tryptophan: C\(_\beta\) is kept as a normal atom and two dummy masses are created at the center of mass of each of the rings, each with a mass equal to the total mass of the respective ring (C\(_{{\delta}2}\) and C\(_{{\epsilon}2}\) are each counted half for each ring). This keeps the overall center of mass and the moment of inertia almost (but not quite) equal to what it was. See Fig. 50 C.
Histidine: C\(_\gamma\), C\(_{{\epsilon}1}\) and N\(_{{\epsilon}2}\) are kept as normal atoms, but with masses redistributed such that the center of mass of the ring is preserved. See Fig. 50 D.