Electric fields#
A pulsed and oscillating electric field can be applied according to:
where \(E_0\) is the field strength, the angular frequency
\(\omega = 2\pi c/\lambda\), \(t_0\) is the time
at of the peak in the field strength and \(\sigma\) is the width of
the pulse. Special cases occur when \(\sigma\) = 0 (non-pulsed
field) and for \(\omega\) is 0 (static field). See
electric-field-x for more details.
This simulated laser-pulse was applied to simulations of melting ice 146. A pulsed electric field may look like Fig. 48. In the supporting information of that paper the impact of an applied electric field on a system under periodic boundary conditions is analyzed. It is described that the effective electric field under PBC is larger than the applied field, by a factor depending on the size of the box and the dielectric properties of molecules in the box. For a system with static dielectric properties this factor can be corrected for. But for a system where the dielectric varies over time, for example a membrane protein with a pore that opens and closes during the simulation, this way of applying an electric field is not useful. In such cases one can use the computational electrophysiology protocol described in the next section (sec. Computational Electrophysiology).
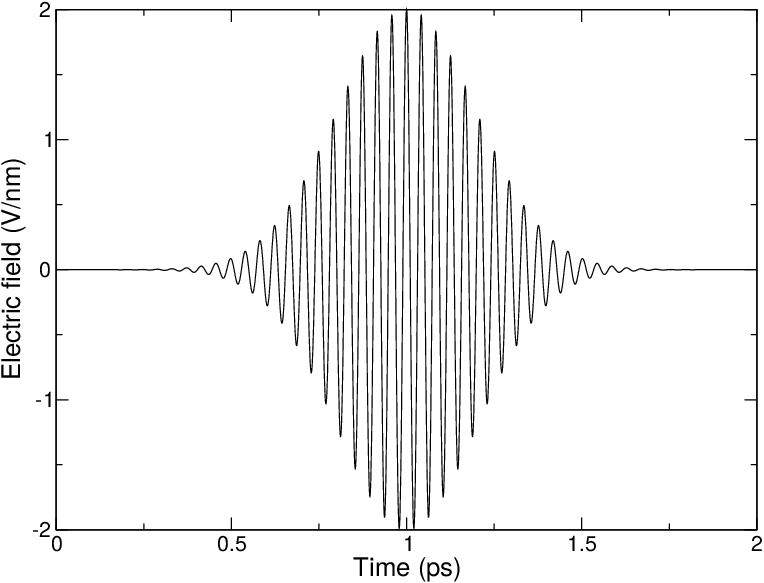
Fig. 48 A simulated laser pulse in GROMACS.#
Electric fields are applied when the following options are specified in the grompp mdp file. You specify, in order, \(E_0\), \(\omega\), \(t_0\) and \(\sigma\):
electric-field-x = 0.04 0 0 0
yields a static field with \(E_0\) = 0.04 V/nm in the X-direction. In contrast,
electric-field-x = 2.0 150 5 0
yields an oscillating electric field with \(E_0\) = 2 V/nm, \(\omega\) = 150/ps and \(t_0\) = 5 ps. Finally
electric-field-x = 2.0 150 5 1
yields an pulsed-oscillating electric field with \(E_0\) = 2 V/nm,
\(\omega\) = 150/ps and \(t_0\) = 5 ps and \(\sigma\) = 1
ps. Read more in ref. 146. Note that the input file
format is changed from the undocumented older version. A figure like
Fig. 48 may be produced by passing the
-field option to gmx mdrun.
Boundary conditions#
In a finite, non-periodic system with plain Coulomb interactions, the application of an electric field is straightforward and one could define a potential energy. But in most cases periodic systems are used. This is problematic, as dipoles will align with the field and build a net dipole in one periodic image. The interactions between this dipole and all its periodic images is a conditionally convergent sum. This leads to the, somewhat strange, effect that the boundary condition at infinity affects the energy of the system and the sampled conformations.
By default, Ewald type electrostatics methods will give a conducting boundary condition. This means that there is no penalty to building up a net dipole. This does not correspond to the situation of putting an electric field on a finite amount of material in an experiment. In fact, the electric field applied in the simulation is larger than that applied to a finite amount of material by a factor of the dielectric constant of the system, which can be rather large. One can correct for this by lowering the applied electric field by the dielectric constant.
When using Ewald type electrostatics, one can directly obtain the correct
average polarization in an electric field by using insulating boundary
conditions by setting epsilon-surface to 1. A disadvantage
of this is that the fluctuations of the polarization are suppressed by
a factor corresponding to the dielectric constant, at least when
the simulated system is supposed to represent a small part of the total
system. In practice, insulating boundary conditions can usually not be
used, as this is only supported when each molecule is a single update
group so molecules are not broken over periodic boundary conditions.
Another issue of periodic boundary conditions is that one can not define a potential energy when charged molecules are present. It would be possible when all molecules are neutral, but in GROMACS this is not done as this would require keeping track of periodic images of parts of molecules. When there are charged molecules in a liquid, a constant electric field will lead to non-equilibrium simulation where the charged molecules move along the field.
It might seem that one can avoid part of these issues by avoiding full-range electrostatics and using reaction-field electrostatics instead. But, apart from the issues with ignoring long-range interactions, there are still similar issues in that the response to the electric field depends on the dielectric permittivity used for the reaction field.