Dihedral principal component analysis

gmx angle, gmx covar, gmx anaeig

Principal component analysis can be performed in dihedral space 172 using GROMACS. You start by defining the dihedral angles of interest in an index file, either using gmx mk_angndx or otherwise. Then you use the gmx angle program with the -or flag to produce a new trr file containing the cosine and sine of each dihedral angle in two coordinates, respectively. That is, in the trr file you will have a series of numbers corresponding to: cos(\(\phi_1\)), sin(\(\phi_1\)), cos(\(\phi_2\)), sin(\(\phi_2\)), …, cos(\(\phi_n\)), sin(\(\phi_n\)), and the array is padded with zeros, if necessary. Then you can use this trr file as input for the gmx covar program and perform principal component analysis as usual. For this to work you will need to generate a reference file (tpr, gro, pdb etc.) containing the same number of “atoms” as the new trr file, that is for \(n\) dihedrals you need 2\(n\)/3 atoms (rounded up if not an integer number). You should use the -nofit option for gmx covar since the coordinates in the dummy reference file do not correspond in any way to the information in the trr file. Analysis of the results is done using gmx anaeig.

Hydrogen bonds

gmx hbond

The program gmx hbond analyzes the hydrogen bonds (H-bonds) between all possible donors D and acceptors A. To determine if an H-bond exists, a geometrical criterion is used, see also Fig. 57:

\[\begin{split}\begin{array}{rclcl} r & \leq & r_{HB} & = & 0.35~\mbox{nm} \\ \alpha & \leq & \alpha_{HB} & = & 30^o \\ \end{array}\end{split}\]

Fig. 57 Geometrical Hydrogen bond criterion.

The value of \(r_{HB} = 0.35 \mathrm{nm}\) corresponds to the first minimum of the RDF of SPC water (see also Fig. 58).

The program gmx hbond analyzes all hydrogen bonds existing between two groups of atoms (which must be either identical or non-overlapping) or in specified donor-hydrogen-acceptor triplets, in the following ways:

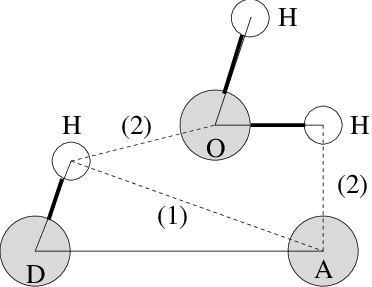
Fig. 58 Insertion of water into an H-bond. (1) Normal H-bond between two residues. (2) H-bonding bridge via a water molecule.

• Donor-Acceptor distance (\(r\)) distribution of all H-bonds

• Hydrogen-Donor-Acceptor angle (\(\alpha\)) distribution of all H-bonds

• The total number of H-bonds in each time frame

• The number of H-bonds in time between residues, divided into groups \(n\)-\(n\)+\(i\) where \(n\) and \(n\)+\(i\) stand for residue numbers and \(i\) goes from 0 to 6. The group for \(i=6\) also includes all H-bonds for \(i>6\). These groups include the \(n\)-\(n\)+\(3\), \(n\)-\(n\)+\(4\) and \(n\)-\(n\)+\(5\) H-bonds, which provide a measure for the formation of \(\alpha\)-helices or \(\beta\)-turns or strands.

• The lifetime of the H-bonds is calculated from the average over all autocorrelation functions of the existence functions (either 0 or 1) of all H-bonds:

  (1)\[C(\tau) ~=~ \langle s_i(t)~s_i (t + \tau) \rangle\]

• with \(s_i(t) = \{0,1\}\) for H-bond \(i\) at time \(t\). The integral of \(C(\tau)\) gives a rough estimate of the average H-bond lifetime \(\tau_{HB}\):

  (2)\[\tau_{HB} ~=~ \int_{0}^{\infty} C(\tau) d\tau\]

• Both the integral and the complete autocorrelation function \(C(\tau)\) will be output, so that more sophisticated analysis (e.g. using multi-exponential fits) can be used to get better estimates for \(\tau_{HB}\). A more complete analysis is given in ref. 173; one of the more fancy option is the Luzar and Chandler analysis of hydrogen bond kinetics 174, 175.

• An H-bond existence map can be generated of dimensions # H-bonds\(\times\)# frames. The ordering is identical to the index file (see below), but reversed, meaning that the last triplet in the index file corresponds to the first row of the existence map.

• Index groups are output containing the analyzed groups, all donor-hydrogen atom pairs and acceptor atoms in these groups, donor-hydrogen-acceptor triplets involved in hydrogen bonds between the analyzed groups and all solvent atoms involved in insertion.