Non-bonded interactions

Non-bonded interactions in GROMACS are pair-additive:

(139)$$V({\mathbf{r}}_1,\dots {\mathbf{r}}_N)=\sum _{i<j}{V}_{ij}({\mathbf{r}}_{ij});$$

(140)$${\mathbf{F}}_i=-\sum _j\frac{d{V}_{ij}(r_{ij})}{d{r}_{ij}}\frac{{\mathbf{r}}_{ij}}{r_{ij}}$$

Since the potential only depends on the scalar distance, interactions will be centro-symmetric, i.e. the vectorial partial force on particle $i$ from the pairwise interaction $V_{ij}(r_{ij})$ has the opposite direction of the partial force on particle $j$. For efficiency reasons, interactions are calculated by loops over interactions and updating both partial forces rather than summing one complete nonbonded force at a time. The non-bonded interactions contain a repulsion term, a dispersion term, and a Coulomb term. The repulsion and dispersion term are combined in either the Lennard-Jones (or 6-12 interaction), or the Buckingham (or exp-6 potential). In addition, (partially) charged atoms act through the Coulomb term.

The Lennard-Jones interaction

The Lennard-Jones potential $V_{LJ}$ between two atoms equals:

(141)$$V_{LJ}(r_{ij})=\frac{C_{ij}^{(12)}}{{r_{ij}}^{12}}-\frac{C_{ij}^{(6)}}{{r_{ij}}^6}$$

See also Fig. 16 The parameters $C_{ij}^{(12)}$ and $C_{ij}^{(6)}$ depend on pairs of atom types; consequently they are taken from a matrix of LJ-parameters. In the Verlet cut-off scheme, the potential is shifted by a constant such that it is zero at the cut-off distance.

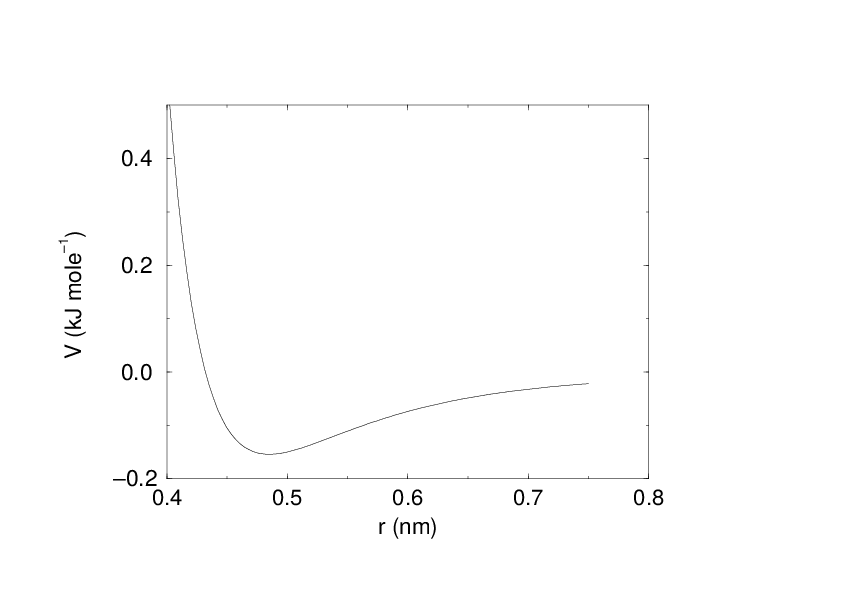
Fig. 16 The Lennard-Jones interaction.

The force derived from this potential is:

(142)$${\mathbf{F}}_i({\mathbf{r}}_{ij})=-(12\frac{C_{ij}^{(12)}}{{r_{ij}}^{13}}-6\frac{C_{ij}^{(6)}}{{r_{ij}}^7})\frac{{\mathbf{r}}_{ij}}{r_{ij}}$$

The LJ potential may also be written in the following form:

(143)$$V_{LJ}({\mathbf{r}}_{ij})=4{ϵ}_{ij}({\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6)$$

In constructing the parameter matrix for the non-bonded LJ-parameters, two types of combination rules can be used within GROMACS, only geometric averages (type 1 in the input section of the force-field file):

(144)$$\begin{array}{r}\begin{array}{rcl}{C}_{ij}^{(6)}& =& {\left(C_{ii}^{(6)}{C}_{jj}^{(6)}\right)}^{1/2}\\ C_{ij}^{(12)}& =& {\left(C_{ii}^{(12)}{C}_{jj}^{(12)}\right)}^{1/2}\end{array}\end{array}$$

or, alternatively the Lorentz-Berthelot rules can be used. An arithmetic average is used to calculate ${\sigma }_{ij}$, while a geometric average is used to calculate ${ϵ}_{ij}$ (type 2):

(145)$$\begin{array}{r}\begin{array}{rcl}{\sigma }_{ij}& =& \frac{1}{2}({\sigma }_{ii}+{\sigma }_{jj})\\ {ϵ}_{ij}& =& {\left({ϵ}_{ii}{ϵ}_{jj}\right)}^{1/2}\end{array}\end{array}$$

finally an geometric average for both parameters can be used (type 3):

(146)$$\begin{array}{r}\begin{array}{rcl}{\sigma }_{ij}& =& {\left({\sigma }_{ii}{\sigma }_{jj}\right)}^{1/2}\\ {ϵ}_{ij}& =& {\left({ϵ}_{ii}{ϵ}_{jj}\right)}^{1/2}\end{array}\end{array}$$

This last rule is used by the OPLS force field.

Buckingham potential

The Buckingham potential has a more flexible and realistic repulsion term than the Lennard-Jones interaction, but is also more expensive to compute. The potential form is:

(147)$$V_{bh}(r_{ij})=A_{ij}\exp (-B_{ij}{r}_{ij})-\frac{C_{ij}}{{r_{ij}}^6}$$

Fig. 17 The Buckingham interaction.

See also Fig. 17. The force derived from this is:

(148)$${\mathbf{F}}_i(r_{ij})=[A_{ij}{B}_{ij}\exp (-B_{ij}{r}_{ij})-6\frac{C_{ij}}{{r_{ij}}^7}]\frac{{\mathbf{r}}_{ij}}{r_{ij}}$$

Coulomb interaction

The Coulomb interaction between two charge particles is given by:

(149)$$V_c(r_{ij})=f\frac{q_i{q}_j}{{\epsilon }_r{r}_{ij}}$$

See also Fig. 18, where $f=\frac{1}{4\pi {\epsilon }_0}=138.935458$ (see chapter Definitions and Units)

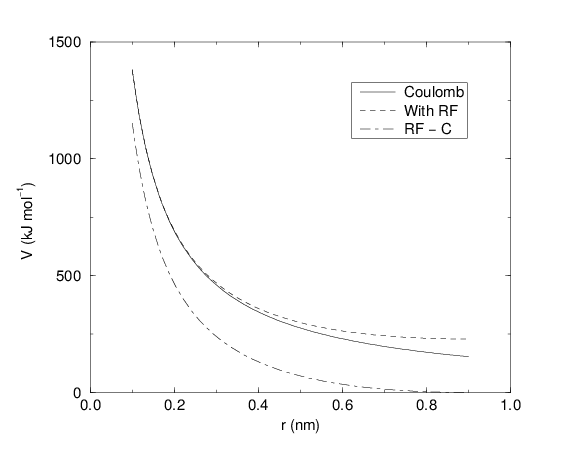
Fig. 18 The Coulomb interaction (for particles with equal signed charge) with and without reaction field. In the latter case ${\epsilon }_r$ was 1, ${\epsilon }_{rf}$ was 78, and $r_c$ was 0.9 nm. The dot-dashed line is the same as the dashed line, except for a constant.

The force derived from this potential is:

(150)$${\mathbf{F}}_i({\mathbf{r}}_{ij})=-f\frac{q_i{q}_j}{{\epsilon }_r{r_{ij}}^2}\frac{{\mathbf{r}}_{ij}}{r_{ij}}$$

A plain Coulomb interaction should only be used without cut-off or when all pairs fall within the cut-off, since there is an abrupt, large change in the force at the cut-off. In case you do want to use a cut-off, the potential can be shifted by a constant to make the potential the integral of the force. With the group cut-off scheme, this shift is only applied to non-excluded pairs. With the Verlet cut-off scheme, the shift is also applied to excluded pairs and self interactions, which makes the potential equivalent to a reaction field with ${\epsilon }_{rf}=1$ (see below).

In GROMACS the relative dielectric constant ${\epsilon }_r$ may be set in the in the input for grompp.

Coulomb interaction with reaction field

The Coulomb interaction can be modified for homogeneous systems by assuming a constant dielectric environment beyond the cut-off $r_c$ with a dielectric constant of ${\epsilon }_{rf}$. The interaction then reads:

(151)$$V_{crf}=f\frac{q_i{q}_j}{{\epsilon }_r{r}_{ij}}[1+\frac{{\epsilon }_{rf}-{\epsilon }_r}{2{\epsilon }_{rf}+{\epsilon }_r}\frac{{r_{ij}}^3}{r_c^3}]-f\frac{q_i{q}_j}{{\epsilon }_r{r}_c}\frac{3{\epsilon }_{rf}}{2{\epsilon }_{rf}+{\epsilon }_r}$$

in which the constant expression on the right makes the potential zero at the cut-off $r_c$. For charged cut-off spheres this corresponds to neutralization with a homogeneous background charge. We can rewrite (151) for simplicity as

(152)$$V_{crf}=f\frac{q_i{q}_j}{{\epsilon }_r}[\frac{1}{r_{ij}}+k_{rf}{r_{ij}}^2-c_{rf}]$$

with

(153)$$\begin{array}{rlr}{k}_{rf}& =& \frac{1}{r_c^3}\frac{{\epsilon }_{rf}-{\epsilon }_r}{(2{\epsilon }_{rf}+{\epsilon }_r)}\end{array}$$

(154)$$\begin{array}{rlr}{c}_{rf}& =& \frac{1}{r_c}+k_{rf}{r}_c^2=\frac{1}{r_c}\frac{3{\epsilon }_{rf}}{(2{\epsilon }_{rf}+{\epsilon }_r)}\end{array}$$

For large ${\epsilon }_{rf}$ the $k_{rf}$ goes to $r_c^{-3}/2$, while for ${\epsilon }_{rf}$ = ${\epsilon }_r$ the correction vanishes. In Fig. 18 the modified interaction is plotted, and it is clear that the derivative with respect to $r_{ij}$ (= -force) goes to zero at the cut-off distance. The force derived from this potential reads:

(155)$${\mathbf{F}}_i({\mathbf{r}}_{ij})=-f\frac{q_i{q}_j}{{\epsilon }_r}[\frac{1}{{r_{ij}}^2}-2k_{rf}{r}_{ij}]\frac{{\mathbf{r}}_{ij}}{r_{ij}}$$

The reaction-field correction should also be applied to all excluded atoms pairs, including self pairs, in which case the normal Coulomb term in (151) and (155) is absent.

Modified non-bonded interactions

In GROMACS, the non-bonded potentials can be modified by a shift function, also called a force-switch function, since it switches the force to zero at the cut-off. The purpose of this is to replace the truncated forces by forces that are continuous and have continuous derivatives at the cut-off radius. With such forces the time integration produces smaller errors. But note that for Lennard-Jones interactions these errors are usually smaller than other errors, such as integration errors at the repulsive part of the potential. For Coulomb interactions we advise against using a shifted potential and for use of a reaction field or a proper long-range method such as PME.

There is no fundamental difference between a switch function (which multiplies the potential with a function) and a shift function (which adds a function to the force or potential) 72. The switch function is a special case of the shift function, which we apply to the force function $F(r)$, related to the electrostatic or van der Waals force acting on particle $i$ by particle $j$ as:

(156)$${\mathbf{F}}_i=cF(r_{ij})\frac{{\mathbf{r}}_{ij}}{r_{ij}}$$

For pure Coulomb or Lennard-Jones interactions $F(r)=F_{\alpha }(r)=\alpha r^{-(\alpha +1)}$. The switched force $F_s(r)$ can generally be written as:

(157)$$\begin{array}{r}\begin{array}{rcl}{F}_s(r)=& F_{\alpha }(r)& r<r_1\\ F_s(r)=& F_{\alpha }(r)+S(r)& r_1\le r<r_c\\ F_s(r)=& 0& r_c\le r\end{array}\end{array}$$

When $r_1=0$ this is a traditional shift function, otherwise it acts as a switch function. The corresponding shifted potential function then reads:

(158)$$V_s(r)={\int }_r^{\mathrm{\infty }}{F}_s(x)dx$$

The GROMACS force switch function $S_F(r)$ should be smooth at the boundaries, therefore the following boundary conditions are imposed on the switch function:

(159)$$\begin{array}{r}\begin{array}{rcl}{S}_F(r_1)& =& 0\\ S_F^{\prime }(r_1)& =& 0\\ S_F(r_c)& =& -F_{\alpha }(r_c)\\ S_F^{\prime }(r_c)& =& -F_{\alpha }^{\prime }(r_c)\end{array}\end{array}$$

A 3${}^{rd}$ degree polynomial of the form

(160)$$S_F(r)=A(r-r_1{)}^2+B(r-r_1{)}^3$$

fulfills these requirements. The constants A and B are given by the boundary condition at $r_c$:

(161)$$\begin{array}{r}\begin{array}{rcl}A& =& -\alpha {\displaystyle \frac{(\alpha +4)r_c-(\alpha +1)r_1}{r_c^{\alpha +2}(r_c-r_1{)}^2}}\\ B& =& \alpha {\displaystyle \frac{(\alpha +3)r_c-(\alpha +1)r_1}{r_c^{\alpha +2}(r_c-r_1{)}^3}}\end{array}\end{array}$$

Thus the total force function is:

(162)$$F_s(r)=\frac{\alpha }{r^{\alpha +1}}+A(r-r_1{)}^2+B(r-r_1{)}^3$$

and the potential function reads:

(163)$$V_s(r)=\frac{1}{r^{\alpha }}-\frac{A}{3}(r-r_1{)}^3-\frac{B}{4}(r-r_1{)}^4-C$$

where

(164)$$C=\frac{1}{r_c^{\alpha }}-\frac{A}{3}(r_c-r_1{)}^3-\frac{B}{4}(r_c-r_1{)}^4$$

The GROMACS potential-switch function $S_V(r)$ scales the potential between $r_1$ and $r_c$, and has similar boundary conditions, intended to produce smoothly-varying potential and forces:

(165)$$\begin{array}{r}\begin{array}{rcl}{S}_V(r_1)& =& 1\\ S_V^{\prime }(r_1)& =& 0\\ S_V^{″}(r_1)& =& 0\\ S_V(r_c)& =& 0\\ S_V^{\prime }(r_c)& =& 0\\ S_V^{″}(r_c)& =& 0\end{array}\end{array}$$

The fifth-degree polynomial that has these properties is

(166)$$S_V(r;r_1,r_c)=1-10{\left(\frac{r-r_1}{r_c-r_1}\right)}^3+15{\left(\frac{r-r_1}{r_c-r_1}\right)}^4-6{\left(\frac{r-r_1}{r_c-r_1}\right)}^5$$

This implementation is found in several other simulation packages,7375 but differs from that in CHARMM.76 Switching the potential leads to artificially large forces in the switching region, therefore it is not recommended to switch Coulomb interactions using this function,72 but switching Lennard-Jones interactions using this function produces acceptable results.

Modified short-range interactions with Ewald summation

When Ewald summation or particle-mesh Ewald is used to calculate the long-range interactions, the short-range Coulomb potential must also be modified. Here the potential is switched to (nearly) zero at the cut-off, instead of the force. In this case the short range potential is given by:

(167)$$V(r)=f\frac{\text{erfc}(\beta r_{ij})}{r_{ij}}{q}_i{q}_j,$$

where $\beta$ is a parameter that determines the relative weight between the direct space sum and the reciprocal space sum and erfc$(x)$ is the complementary error function. For further details on long-range electrostatics, see sec. Long Range Electrostatics.