Bonds/distances, angles and dihedrals¶
[ bonds_1 ]
1 2
3 4
9 10
[ bonds_2 ]
12 13
Selections are also supported, with first two positions defining the first distance, second pair of positions defining the second distance and so on. You can calculate the distances between CA and CB atoms in all your residues (assuming that every residue either has both atoms, or neither) using a selection such as:
name CA CB
The selections also allow more generic distances to be computed. For example, to compute the distances between centers of mass of two residues, you can use:
com of resname AAA plus com of resname BBB
The program gmx angle calculates the distribution of angles and dihedrals in time. It also gives the average angle or dihedral. The index file consists of triplets or quadruples of atom numbers:
[ angles ]
1 2 3
2 3 4
3 4 5
[ dihedrals ]
1 2 3 4
2 3 5 5
For the dihedral angles you can use either the “biochemical convention” (\(\phi = 0 \equiv cis\)) or “polymer convention” (\(\phi = 0 \equiv trans\)), see Fig. 55.
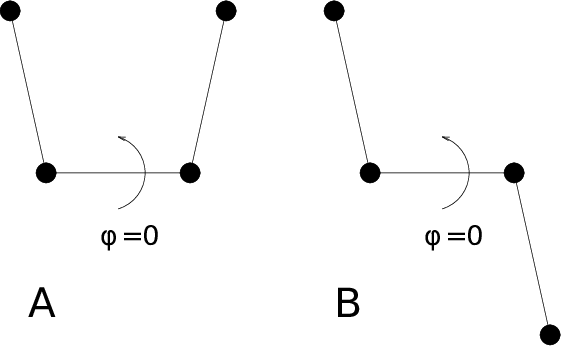
Fig. 55 Dihedral conventions: A. “Biochemical convention”. B. “Polymer convention”.¶
The program gmx gangle provides a selection-enabled version to compute angles. This tool can also compute angles and dihedrals, but does not support all the options of gmx angle, such as autocorrelation or other time series analyses. In addition, it supports angles between two vectors, a vector and a plane, two planes (defined by 2 or 3 points, respectively), a vector/plane and the \(z\) axis, or a vector/plane and the normal of a sphere (determined by a single position). Also the angle between a vector/plane compared to its position in the first frame is supported. For planes, gmx gangle uses the normal vector perpendicular to the plane. See Fig. 56 A, B, C) for the definitions.
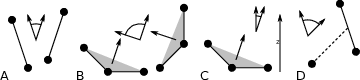
Fig. 56 Angle options of gmx gangle: A. Angle between two vectors. B. Angle between two planes. C. Angle between a vector and the \(z\) axis. D. Angle between a vector and the normal of a sphere. Also other combinations are supported: planes and vectors can be used interchangeably.¶